אי-ודאות, זמינות, והפקת אנרגיה בין-פלנטרית
ראיון עם פרופ' בני נתן
ראיון עם פרופ' בני נתן
לפי הדטרמיניזם, ישנו קשר רציף בין אירוע לאירוע, ודבר אחד מביא לשני. זהו רעיון פילוסופי עם אספקטים תיאולוגיים ומדעים עוד מהמאה ה-14 שהיו לו תומכים רבים. מבחינה מדעית, גישה זו אומרת שאם כל התנאים בזמן מסוים ידועים לנו (תנאי התחלה), ניתן לדעת מה יהיה המצב רגע אחרי זה. זהו הרעיון מאחורי המכניקה הניוטונית.
"עקרון אי-הודאות של הייזנברג, שפורסם ב-1927, סתר את הדטרמיניזם [א]. יש לציין שאיינשטיין התקשה לקבל תמונת מצב של עולם אקראי ("אלוהים אינו משחק בקוביה" ) והעבודה המפורסמת ביותר כנגד עקרון אי הוודאות ומכניקת הקוונטים [ב] היא פרדוקס EPR [ג].
ידוע כי בהטלת מטבע ההסתברות לקבלת אחד הצדדים היא 50%. האומנם? לו ידענו בדיוק מהו הכוח המופעל על המטבע, מהי זווית ההטלה, מהי התצורה האוירודינמית המדויקת של המטבע וכו' יכולנו לדעת בהסתברות של 100% על איזה צד הוא ייפול. ההסתברות של 50% נובעת מאי הידיעה של "גורמים חבויים" ואקראיים שאין עליהם שליטה.
"שאלה שנשאלה: האם יש גורמים חבויים שמשפיעים על החלקיק הבודד? האם אי הודאות במקום החלקיק נובעת מגורמים לא ידועים? אם היינו יודעים הכל על היקום אז לא היה צורך בהסתברות (כך טענו הדטרמיניסטים).
יש תאוריות שאומרות שהגורמים החבויים לא קיימים ושהעולם אקראי. היום מקובלת השקפה שהעולם איננו דטרמיניסטי. אבל האם העולם אקראי לחלוטין? לא. אמנם ייתכן מצב-קצה שבו אירוע נדיר כמו גשם טרופי במדבר גובי יקרה, אבל בפועל, אירוע כזה לא יתרחש."
כיצד תיתכן שבירת החוק השני בעולם המיקרוסקופי? "הגישה של התורה הקוונטית היא הסתברותית. פילוג ההסתברות מצביע חד משמעית על סיכוי אפס לכל החלקיקים לנוע לכיוון אחד. החוק השני מתייחס למקרו ולא למיקרו. אין אפשרות לדעת את מהירותה של המולקולה הבודדת אבל כן ניתן לדעת מה יהיה הגודל הממוצע של המהירות של המולקולות."
"החוק השני [ד] של התרמודינמיקה נוסח בצורתו הסופית בשנת 1965 ע"י חצופולוס וקינן: "כל מערכת חייבת להגיע למצב שיווי משקל אחד ויחיד". ניסוח זה פורסם הרבה אחרי התפתחות התורה הקוונטית (תחילת המאה ה-20).
"עקרון אי-הודאות של הייזנברג, שפורסם ב-1927, סתר את הדטרמיניזם [א]. יש לציין שאיינשטיין התקשה לקבל תמונת מצב של עולם אקראי ("אלוהים אינו משחק בקוביה" ) והעבודה המפורסמת ביותר כנגד עקרון אי הוודאות ומכניקת הקוונטים [ב] היא פרדוקס EPR [ג].
ידוע כי בהטלת מטבע ההסתברות לקבלת אחד הצדדים היא 50%. האומנם? לו ידענו בדיוק מהו הכוח המופעל על המטבע, מהי זווית ההטלה, מהי התצורה האוירודינמית המדויקת של המטבע וכו' יכולנו לדעת בהסתברות של 100% על איזה צד הוא ייפול. ההסתברות של 50% נובעת מאי הידיעה של "גורמים חבויים" ואקראיים שאין עליהם שליטה.
"שאלה שנשאלה: האם יש גורמים חבויים שמשפיעים על החלקיק הבודד? האם אי הודאות במקום החלקיק נובעת מגורמים לא ידועים? אם היינו יודעים הכל על היקום אז לא היה צורך בהסתברות (כך טענו הדטרמיניסטים).
יש תאוריות שאומרות שהגורמים החבויים לא קיימים ושהעולם אקראי. היום מקובלת השקפה שהעולם איננו דטרמיניסטי. אבל האם העולם אקראי לחלוטין? לא. אמנם ייתכן מצב-קצה שבו אירוע נדיר כמו גשם טרופי במדבר גובי יקרה, אבל בפועל, אירוע כזה לא יתרחש."
כיצד תיתכן שבירת החוק השני בעולם המיקרוסקופי? "הגישה של התורה הקוונטית היא הסתברותית. פילוג ההסתברות מצביע חד משמעית על סיכוי אפס לכל החלקיקים לנוע לכיוון אחד. החוק השני מתייחס למקרו ולא למיקרו. אין אפשרות לדעת את מהירותה של המולקולה הבודדת אבל כן ניתן לדעת מה יהיה הגודל הממוצע של המהירות של המולקולות."
"החוק השני [ד] של התרמודינמיקה נוסח בצורתו הסופית בשנת 1965 ע"י חצופולוס וקינן: "כל מערכת חייבת להגיע למצב שיווי משקל אחד ויחיד". ניסוח זה פורסם הרבה אחרי התפתחות התורה הקוונטית (תחילת המאה ה-20).
היכן בחיי היומיום ניתן לחוות את מושג האנטרופיה [ה]?
האנטרופיה מוגדרת
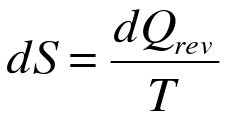
אם מתייחסים למאגר חום, דהיינו מאגר מספיק גדול כך שהטמפרטורה שלו אינה משתנה ולא משנה מהי כמות החום הנכנס או יוצא ממנו, אין זה משנה למאגר אם התהליך הפיך או בלתי הפיך. אם טמפרטורה של אדם בריא היא 36°C , כלומר 309K, והוא שם את כף ידו, למשך עשירית השניה על מחבת בטמפ' 573K, שמעבירה לו חום בקצב של 3 kW (3 kJ/s), אז השינוי באנטרופיה של האיש שווה ל-
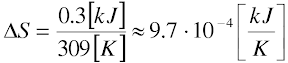
והשינוי באנטרופיה של המחבת שווה ל-
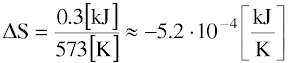
שים לב כי סה"כ האנטרופיה גדלה! זוהי דוגמה לתהליך בלתי הפיך.
המושג של אנטרופיה איננו פשוט אבל זהו עניין של הרגל. האם המושג של אנרגיה פשוט יותר? לא! אבל אנו רגילים אליו ונשמע פשוט. אני מעולם לא יצאתי מהבית ופגשתי גוש של אנרגיה.
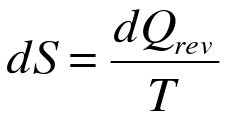
אם מתייחסים למאגר חום, דהיינו מאגר מספיק גדול כך שהטמפרטורה שלו אינה משתנה ולא משנה מהי כמות החום הנכנס או יוצא ממנו, אין זה משנה למאגר אם התהליך הפיך או בלתי הפיך. אם טמפרטורה של אדם בריא היא 36°C , כלומר 309K, והוא שם את כף ידו, למשך עשירית השניה על מחבת בטמפ' 573K, שמעבירה לו חום בקצב של 3 kW (3 kJ/s), אז השינוי באנטרופיה של האיש שווה ל-
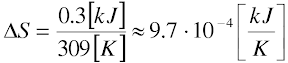
והשינוי באנטרופיה של המחבת שווה ל-
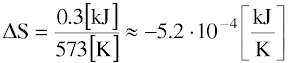
שים לב כי סה"כ האנטרופיה גדלה! זוהי דוגמה לתהליך בלתי הפיך.
המושג של אנטרופיה איננו פשוט אבל זהו עניין של הרגל. האם המושג של אנרגיה פשוט יותר? לא! אבל אנו רגילים אליו ונשמע פשוט. אני מעולם לא יצאתי מהבית ופגשתי גוש של אנרגיה.
האם ש"מ פירושו מוות טוטאלי? כלומר שלא ניתן ליצור סדר חדש מהתוצרים שקבלנו?
בעיקרון שיווי משקל מהווה חוסר כל תנועה וזהו כן מוות. החוק השני דוחף אותנו לכך. אבל בכל זאת אנו בונים סדר ומערכות מסודרות. עושים זאת ע"י השקעת עבודה וצורכים אנרגיה. אם לא ניזונים, פשוט מתים! ב-1977 מקרידקיס, עוד יווני, פרסם מאמר בשם "החוק השני של המערכות" בו הוא מצביע על השאיפה הטבעית ליצור מערכות מסודרות בו בזמן שהחוק השני דוחף להרס הסדר. הטבע מצליח ליצור מערכות כאלה אבל משלמים בצריכת אנרגיה. כך או כך, בסופו של דבר מתים.
מה קורה באפס המוחלט?
"מתקבל מצב לכאורה פרדוקסאלי שלו ניתן היה להגיע לאפס המוחלט יכולנו להפעיל מכונת קרנו בה כמות החום היוצא היה אפס: TL=0 ו-
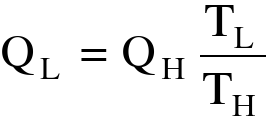
במקרה זה היינו מקבלים עבודה עם מאגר חום יחיד ומפרים ע"י כך את הניסוח של קלוין-פלאנק של החוק השני [ו]. כלומר, האפס המוחלט קיים אבל לא ניתן להגיע אליו."
מה קורה באפס המוחלט?
"מתקבל מצב לכאורה פרדוקסאלי שלו ניתן היה להגיע לאפס המוחלט יכולנו להפעיל מכונת קרנו בה כמות החום היוצא היה אפס: TL=0 ו-
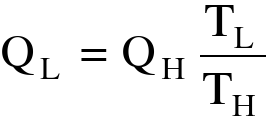
במקרה זה היינו מקבלים עבודה עם מאגר חום יחיד ומפרים ע"י כך את הניסוח של קלוין-פלאנק של החוק השני [ו]. כלומר, האפס המוחלט קיים אבל לא ניתן להגיע אליו."
זמינות
"הבעיה בניצול מרבי של אנרגיה היא בעיה של זמינות. עד כמה ניתן לנצל מערכת מסויימת? אם ניקח גז (משוכלל) ב-1000K שנמצא בלחץ אטמוספרי, ואם ניקח אותו גז באותה טמפרטורה אבל בלחץ 100 אטמ', שניהם זהים מבחינה אנרגטית [ז]. מבחינת הזמינות (כמה עבודה ניתן להפיק) ? ב-100 אטמ' הזמינות של הגז גבוהה יותר. כלומר, הזמינות נקבעת לפי ההבדלים בין המערכת לסביבה.
לו חיינו בעולם קר יותר, יכולנו לבנות תחנת כוח שהנצילות שלה יותר גבוהה כי אז הסביבה הייתה קרה יותר (בהנחה ששורפים נפט באותם תנאים). בקיצור: בכוכב אחר היינו מקבלים נצילות אחרת."
לו חיינו בעולם קר יותר, יכולנו לבנות תחנת כוח שהנצילות שלה יותר גבוהה כי אז הסביבה הייתה קרה יותר (בהנחה ששורפים נפט באותם תנאים). בקיצור: בכוכב אחר היינו מקבלים נצילות אחרת."
בכל פעולה של הפקת אנרגיה מתרחש "מאחורי הקלעים" תהליך של מעבר חום בין מאגרים?
"לא. אנרגיית רוח למשל מסובבת ישר טורבינה, ללא מאגרים, המייצרת אנרגיה חשמלית. אבל אם נלך מספיק רחוק, נוכל לומר כי תנועת האוויר נוצרת מהפרשי טמפרטורה על כדור הארץ, שנגרמים עקב השמש, כך שהמאגר החם הוא השמש והמאגר הקר הוא כדור הארץ, בדומה לתהליך של הפקת אנרגיה ע"י פאנלים סולריים. אבל זוהי הכללה גסה."
אז למה שלא נפיק אנרגיה בכוכב אחר, ונביא אותה לכאן?
"נניח שהטענת סוללות בכוכב אחר בנצילות גבוהה יותר. כדי להביא אותן לפה, יתכן שתצטרך לשלם ביותר אנרגיה מזו שהרווחת, על מנת להיחלץ מהשדה הגרביטציוני ועוד."
בוחן פתע!
מה אתה עושה במחקר הנוכחי שלך?
הודפים ג'ליים. יש להם יתרונות מובהקים מבחינת בטיחות וביצועים. הם דולפים מעט מאד במקרה של פגיעה במיכלים, הם פחות רגישים מהודפים מוצקים, מאפשרים ויסות דחף כמו הנוזליים וניתן לזרות בהם חלקיקי מתכת ולהגדיל ע"י כך את האנרגטיות שלהם. הפרויקט הנוכחי הוא מנוע מגח עם ג'ל וחלקיקי מתכות, ואולי זה יהיה פרויקט לסטודנטים.
אם היה לך בן/בת יחיד/ה, מה היית ממליץ לו/לה ללמוד?
מה שהיא או הוא רוצה, מה שיש בלב, זה מה שאני אומר לילדים שלי. ההמלצה היחידה היא לבחור מקום טוב אוניברסיטה טובה, כי סביבה אינטלקטואלית מעודדת פיתוח רעיונות ומקדמת את האדם. צריך ללמוד ולקבל כלים.
איזו משוואה תיקח לאי בודד?
אם יש משהו שאני אקח זה הניסוח של החוק השני שאומר שכל מערכת שואפת להגיע למצב שווי משקל אחד ויחיד. הייתי לוקח לכל מקום. עם זה אפשר לנתח את העולם.
הערות
[א]. עקרון אי הודאות: עקרון יסוד בפיזיקה קוונטית, הקובע כי לא ניתן לקבוע במקביל ערכים מדויקים לזוגות משתנים מדידים מסוימים של חלקיק אלמנטרי יחיד, אפילו באמצעות כלי מדידה מדויקים עד אין סוף. (מתוך ויקיפדיה)
[ב]. מכניקת הקוונטים היא תורה פיזיקלית הסתברותית-סטטיססטית. אי-אפשר לדעת ממנה איזה תוצאה תתקבל בניסוי אלא רק את ההסתברות לקבל אותה.
[ג]. הפרדוקס קרוי על שמם של אלברט איינשטיין, בוריס פודולסקי ונתן רוזן, שלושת הפיזיקאים שפירסמו פרדוקס זה, בשנת 1935, במאמר שכותרתו "האם תיאור קוונטי של המציאות הפיזיקלית יכול להיחשב שלם?". הפרדוקס ממקד את תשומת הלב לתופעה ידועה במכניקת הקוונטים, לפיה מאורעות המתרחשים במרחק זה מזה משפיעים מיידית זה על זה, חרף המרחק המפריד ביניהם. תוצאה זו נמצאת בסתירה ל"עקרון הלוקליות" הקלאסי לפיו שינוי במערכת מסוימת לא ישפיע מיידית על מערכת אחרת המרוחקת ממנה. תורת היחסות הפרטית קובעת את מהירות האור כגבול עליון למהירות ההשפעה - לא רק חומר אלא אפילו מידע לא יכול לנוע מעל מהירות זו. (ויקיפדיה)
[ד]. החוק השני של התרמודינמיקה גורר, בין היתר, שלא ניתן לבצע עבודה (כלומר להפיק אנרגיה שימושית) ממערכת פיזיקלית המכילה רק גז בטמפרטורה ולחץ אחידים.
[ה]. אנטרופיה היא מדד אדדיטיבי לריבוי המצבים המיקרוסקופיים האפשריים של המערכת עבור מצב מקרוסקופי נתון. לודוויג בולצמן קשר אותה למספר המצבים המיקרוסקופיים השונים שיכולים לתת אותו מצב מקרוסקופי:
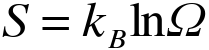
האנטרופיה היא אפס כאשר המערכת נמצאת בודאות במצב אחד, והיא הגבוהה ביותר כאשר הסיכוי להיות בכל מצב הוא שווה.
[ו]. ניסוח קלוין-פלאנק: לא קיימת מכונה מחזורית הקולטת חום ממאגר חום יחיד, ומפיקה כמות שווה של עבודה.
[ז]. בגז אידאלי, האנרגיה תלויה בסוג הגז ובטמפרטורה בלבד
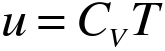
[ב]. מכניקת הקוונטים היא תורה פיזיקלית הסתברותית-סטטיססטית. אי-אפשר לדעת ממנה איזה תוצאה תתקבל בניסוי אלא רק את ההסתברות לקבל אותה.
[ג]. הפרדוקס קרוי על שמם של אלברט איינשטיין, בוריס פודולסקי ונתן רוזן, שלושת הפיזיקאים שפירסמו פרדוקס זה, בשנת 1935, במאמר שכותרתו "האם תיאור קוונטי של המציאות הפיזיקלית יכול להיחשב שלם?". הפרדוקס ממקד את תשומת הלב לתופעה ידועה במכניקת הקוונטים, לפיה מאורעות המתרחשים במרחק זה מזה משפיעים מיידית זה על זה, חרף המרחק המפריד ביניהם. תוצאה זו נמצאת בסתירה ל"עקרון הלוקליות" הקלאסי לפיו שינוי במערכת מסוימת לא ישפיע מיידית על מערכת אחרת המרוחקת ממנה. תורת היחסות הפרטית קובעת את מהירות האור כגבול עליון למהירות ההשפעה - לא רק חומר אלא אפילו מידע לא יכול לנוע מעל מהירות זו. (ויקיפדיה)
[ד]. החוק השני של התרמודינמיקה גורר, בין היתר, שלא ניתן לבצע עבודה (כלומר להפיק אנרגיה שימושית) ממערכת פיזיקלית המכילה רק גז בטמפרטורה ולחץ אחידים.
[ה]. אנטרופיה היא מדד אדדיטיבי לריבוי המצבים המיקרוסקופיים האפשריים של המערכת עבור מצב מקרוסקופי נתון. לודוויג בולצמן קשר אותה למספר המצבים המיקרוסקופיים השונים שיכולים לתת אותו מצב מקרוסקופי:
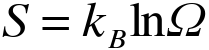
האנטרופיה היא אפס כאשר המערכת נמצאת בודאות במצב אחד, והיא הגבוהה ביותר כאשר הסיכוי להיות בכל מצב הוא שווה.
[ו]. ניסוח קלוין-פלאנק: לא קיימת מכונה מחזורית הקולטת חום ממאגר חום יחיד, ומפיקה כמות שווה של עבודה.
[ז]. בגז אידאלי, האנרגיה תלויה בסוג הגז ובטמפרטורה בלבד
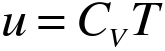
אין תגובות:
הוסף רשומת תגובה